Introduction to VC dimension
Matthieu R Bloch
RECAP: The learning problem
- Dataset \(\calD\eqdef\{(\bfx_1,y_1),\cdots,(\bfx_N,y_N)\}\)
- \(\{\bfx_i\}_{i=1}^N\) drawn i.i.d. from unknown \(P_{\bfx}\) on \(\calX\)
- \(\{y_i\}_{i=1}^N\) labels with \(\calY=\{0,1\}\) (binary classification)
Unknown \(f:\calX\to\calY\), no noise.
Finite set of hypotheses \(\calH\), \(\card{\calH}=M<\infty\)
- \(\calH\eqdef\{h_j\}_{j=1}^M\)
Binary loss function \(\ell:\calY\times\calY\rightarrow\bbR^+:(y_1,y_2)\mapsto \indic{y_1\neq y_2}\)
True risk and empirical risk: \[ R(h)\eqdef\P[\bfx y]{h(\bfx)\neq y}\qquad \widehat{R}_N(h)=\frac{1}{N}\sum_{i=1}^{N} \indic{h(\bfx_i)\neq y} \]
We want to understand when \(\widehat{R}_N(h^*)\approx R(h^*)\) where \(h^*=\argmin_{h\in\calH}\widehat{R}_N(h)\)
Generalization bounds
For a hypothesis set \(\calH\) with \(\card{\calH}=M\) we showed that \[ \forall\epsilon>0\quad\P{\abs{\widehat{R}_N(h^*)-{R}(h^*)}\geq\epsilon}\leq 2M\exp(-2N\epsilon^2)\]
We used the union bound to introduced the factor \(M\); for any \(\epsilon>0\) \[\P{\abs{\widehat{R}_N(h^*)-{R}(h^*)}\geq\epsilon}\leq \P{\max_{h\in\calH}\abs{\widehat{R}_N(h)-{R}(h)}\geq\epsilon} \leq \sum_{j=1}^M\P{\abs{\widehat{R}_N(h_j)-{R}(h_j)}\geq\epsilon}\]
The second inequality is tight if the events \(\calE_j\eqdef \{\abs{\widehat{R}_N(h_j)-{R}(h_j)}\geq\epsilon\}\) are disjoint
Events are not at all disjoint when classifying
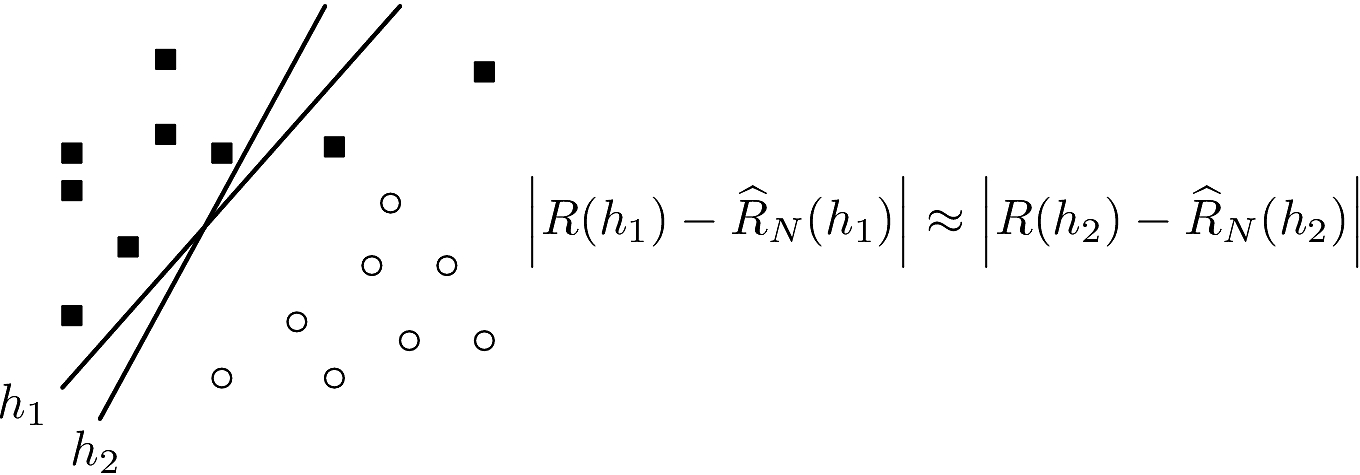
Dichotomy
The union bound naturally depends on the size of \(\calH\), but this is not what matters
We will consider the number of hypotheses that lead to distinct labeling for a dataset
For a dataset \(\calD\eqdef \{\bfx_i\}_{i=1}^N\) and set of hypotheses \(\calH\), the set of dichotomies generated by \(\calH\) on \(\calD\) is \[\calH(\{\bfx_i\}_{i=1}^N)\eqdef \{\{h(\bfx_i)\}_{i=1}^N:h\in\calH\}\]
By definition \(\card{\calH(\{\bfx_i\}_{i=1}^N)}\leq 2^N\) and in general \(\card{\calH(\{\bfx_i\}_{i=1}^N)}\ll\card{\calH}\)
For a set of hypotheses \(\calH\), the growth function of \(\calH\) is \[m_\calH(N)\eqdef\max_{\{\bfx_i\}_{i=1}^N}\card{\calH(\{\bfx_i\}_{i=1}^N)}\]
The growth function does not depend on the datapoints \(\{\bfx_i\}_{i=1}^N\) and \(m_{\calH}(N)\leq 2^N\)
Examples
- Positive rays: \(\calH\eqdef\{h:\bbR\to\{\pm 1\}:x\mapsto \sgn{x-a}| a\in\bbR\}\)

\[m_\calH = N+1\]
Positive intervals: \(\calH\eqdef\{h:\bbR\to\{\pm 1\}:x\mapsto \indic{x\in[a;b]}-\indic{x\notin[a;b]}| a<b\in\bbR\}\)
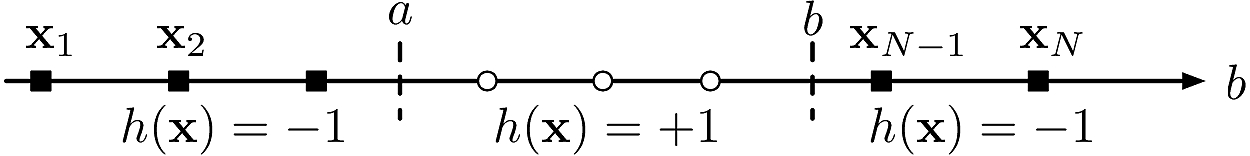
- \[m_\calH = {N+1 \choose 2}+1 = \frac{1}{2}N^2+\frac{1}{2}N+1\]
Examples
- Convex sets: \(\calH\eqdef\{h:\bbR^2\to\{\pm 1\}| \{\bfx\in\bbR^2:h(\bfx)=+1\}\textsf{ is convex}\}\)
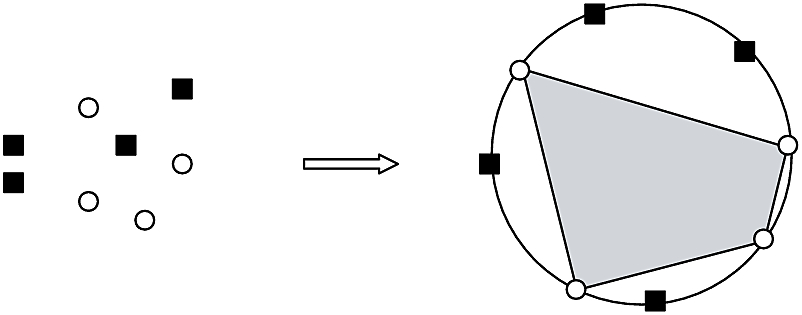
\(m_\calH(N)=2^N\) because we can generate all dichotomies
If \(\calH\) can generate all dichotomies on \(\{\bfx_i\}_{i=1}^N\), we say that \(\calH\) shatters \(\{\bfx_i\}_{i=1}^N\)
Examples
- Linear classifiers: \(\calH\eqdef\{h:\bbR^2\to\{\pm 1\}:\bfx\mapsto\sgn{\bfw^\intercal\bfx+b}| \bfw\in\bbR^2,b\in\bbR\}\)
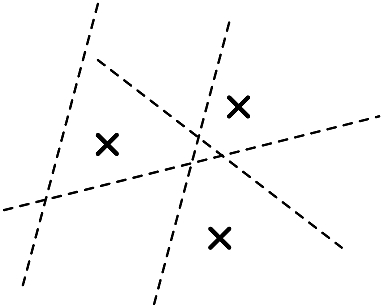
- The growth function is a worst case measure, hence \(m_{\calH}(3)=8\)

- 4 points cannot always be shattered and \(m_{\calH}(4)=14<2^4\)
Wishful thinking
The growth function \(m_\calH\) can sometimes be smaller than \(\card{\calH}\)
What if we could use \(m_\calH\) instead of \(\card{\calH}\) in our analysis?
We know that with probability at least \(1-\delta\) \[{R}(h^*)\leq \widehat{R}_N(h^*) +\sqrt{\frac{1}{2N}\log\frac{2\card{\calH}}{\delta}}\]
What if we could show that with probability at least \(1-\delta\) \[{R}(h^*)\leq \widehat{R}_N(h^*) +\sqrt{\frac{1}{2N}\log\frac{2m_\calH(N) }{\delta}} \qquad?\]
- Our ability to generalize then depend on the behavior of the growth function
- If \(m_{\calH}(N)\) is exponential in \(N\), we can’t say much
- If \(m_{\calH}(N)\) is polynomial in \(N\), then \({R}(h^*)\approx \widehat{R}_N(h^*)\) for large enough \(N\)
Break points
If not data set of size \(k\) can be shattered by \(\calH\), then \(k\) is a break point for \(\calH\)
If \(k\) is a break point then \(m_\calH(k)<2^k\)
- Examples
- Positive rays: break point \(k=2\)
- Postive Intervals: break point \(k=3\)
- Convex sets: break point \(k=\infty\)
- Linear classifiers: break point \(k=4\)
We will spend some time proving the following result
If there exists any break point for \(\calH\), then \(m_{\calH}(N)\) is polynomial in \(N\)
If there is no break point for \(\calH\), then \(m_{\calH}(N)=2^N\)
Break points
Assume \(\calH\) has break point \(k\). \(B(N,k)\) is the maximum number of dichotomies of \(N\) points such that no subset of size \(k\) can be shattered by the dichotomies.
\(B(N,k)\) is a purely combinatorial quantity, does not depend on \(\calH\)
Assume \(\calH\) has break point \(2\). How many dichotomies can we generate of set of size 3?
By definition, if \(k\) is a break point for \(\calH\), then \(m_\calH(N)\leq B(N,k)\)
Sauer’s lemma
\(B(N,1)=1\), \(B(1,k)=2\) for \(k>1\), \[\forall k>1\quad B(N,k)\leq B(N-1,k) + B(N-1,k-1)\]
\[B(N,k)\leq \sum_{i=0}^{k-1}{N\choose i}\]
\(B(N,k)\) is polynomial in \(N\) of degree \(k-1\)
Conclusion: if \(\calH\) has a break point, \(m_\calH(N)\) is polynomial in \(N\)