Filter methods

Matthieu Bloch

Filtering

  • Feature selection by eliminating irrelevant features
    • objective is to reduce computational complexity, regularize, and retain interpretability
  • Features ranked by order of importance and best \(k\) features are retained
    • “Importance” related to ability to predict \(y_i\) in supervised learning
    • +: usually reasonably fast
    • -: \(k\) best features may not be best \(k\) features
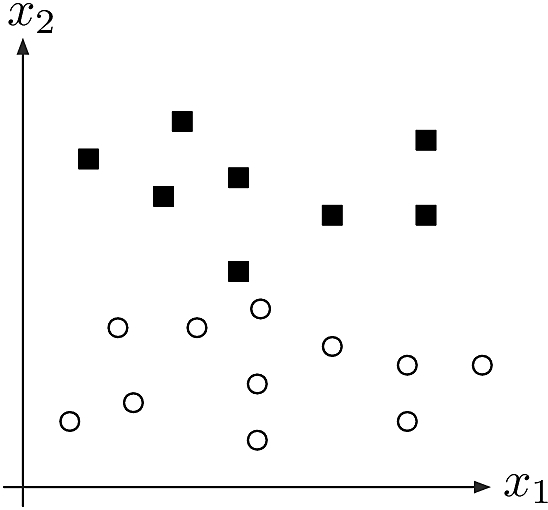
Image Image
Example of feature selection for classification and regression

Ranking for filtering in classification

  • Many possibilities to assign a rank \(r(j)\) to feature \(j\)

  • Misclassification rate: \[r(j)\eqdef\frac{1}{N}\sum_{i=1}^N\indic{y_i\neq\theta(x_{i,j})}\quad\textsf{for some classifier}\quad \theta\]

  • Two-sample t-test statistics: \[r(j)\eqdef \frac{\abs{\overline{x_j^{+}}-\overline{x_j^{-}}}}{s/\sqrt{n}}\] where \(\overline{x_j^{(\pm)}}\) are class means for feature \(j\) and \(s\) is the pooled sample standard deviation

  • Margin: for separable data, compute \[ r(j)\eqdef \min_{k:y_k=+1,\ell:y_\ell=-1}\abs{x_{k,j}-x_{l,j}}\] or order statistics if data is not separable (to ignore outliers)

Ranking for filtering in regression

  • Again many possibilities

  • Correlation coefficient: \[r(j)\eqdef \abs{\rho(j)}\textsf{ with }\rho(j)\eqdef\frac{\textsf{Cov}(x_j,y)}{\sqrt{\Var{x_j}\Var{y}}}\] with sample estimates

  • Mutual information: \[I(X;Y)=\sum_{x,y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}\] measures how much \(x\) tells us about \(y\). Could rank features with \[r(j)\eqdef I(x_j;y)\] using estimates of probabilities

Avoiding redundant features

  • Ranking is legitimate but can lead to selection of redundant features

  • One solution is incremental maximization

  • Example: incremental maximization with mutual information
    • Assume features \(x_{j_1},\cdots,x_{j_{k-1}}\) selected
    • Select \(k\)th feature to maximize \[I(x_{j_k};y)-\beta \sum_{i=1}^{k-1}I(x_{j_k};x_{j_i})\]

  • Biggest drawback to filtering is inability to capture interactions between features

  • Solution 1: wrapper methods based on measure of performance for subset of features and search
    • +: captures interactions
    • -: can be very slow
    • Examples: forward selection, backward elimination
  • Solution 2: embedded methods based on joint feature selection and model fitting
    • Example: LASSO