Stability and Numerical Aspects of Least Squares
Dr. Matthieu R Bloch
Monday, November 29, 2021
Logistics
General announcements
Assignment 6 posted (last assignment)
Due December 7, 2021 for bonus, deadline December 10, 2021
3 lectures left
Let me know what’s missing
Midterm 2 / Assignment 5
- Grades posted this week
What’s on the agenda for today?

Last time:
- Numerical considerations
Today:
- (Fast discussion) of additional numerical considerations
Reading: lecture notes 14/15/16
Easy systems
- Diagonal system
- \(\bfA\in\bbR^{n\times n}\) invertible and diagonal
- \(O(n)\) complexity
- Orthogonal system
- \(\bfA\in\bbR^{n\times n}\) invertible and orthogonal
- \(O(n^2)\) complexity
- Lower triangular system
- \(\bfA\in\bbR^{n\times n}\) invertible and lower diagonal
- \(O(n^2)\) complexity
- General strategy: factorize \(\matA\) to recover some of the structures above
Factorizations
LU factorization
Cholesky factorization
QR decomposition
SVD and eigenvalue decompositions
Computing eigenvalue decompositions for symetric matrices
- Many techniques: we shall only discuss one based on power iterations
Components of supervised machine learning
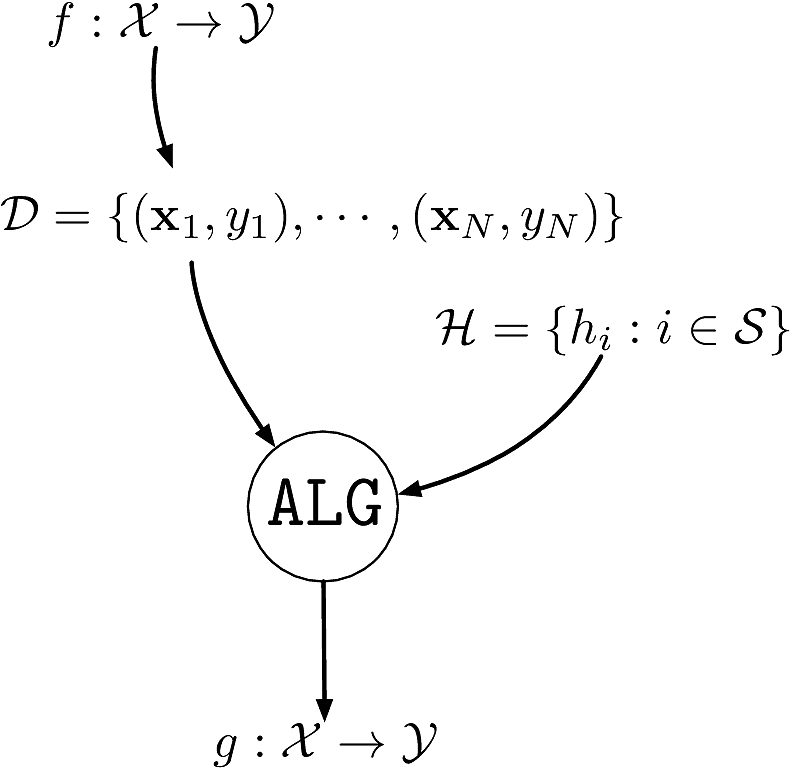
- An unknown function \(f:\calX\to\calY:\bfx\mapsto y=f(\bfx)\) to learn
- The formula to distinguish cats from dogs
- A dataset \(\calD\eqdef\{(\bfx_1,y_1),\cdots,(\bfx_N,y_N)\}\)
- \(\bfx_i\in\calX\eqdef\bbR^d\): picture of cat/dog
- \(y_i\in\calY\eqdef\bbR\): the corresponding label cat/dog
- A set of hypotheses \(\calH\) as to what the function could be
- Example: deep neural nets with AlexNet architecture
- An algorithm \(\texttt{ALG}\) to find the best \(h\in\calH\) that explains \(f\)
- Terminology:
- \(\calY=\bbR\): regression problem
- \(\card{\calY}<\infty\): classification problem
- \(\card{\calY}=2\): binary classification problem
- The goal is to generalize, i.e., be able to classify inputs we have not seen.
A learning puzzle
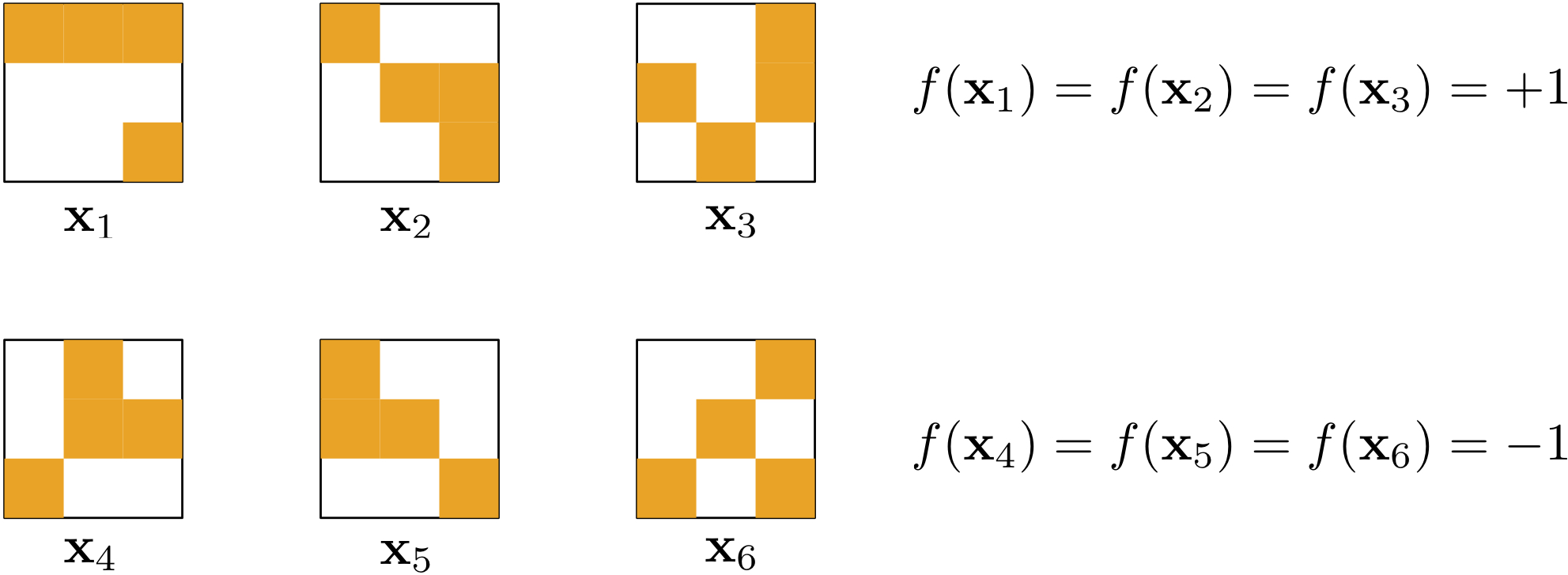
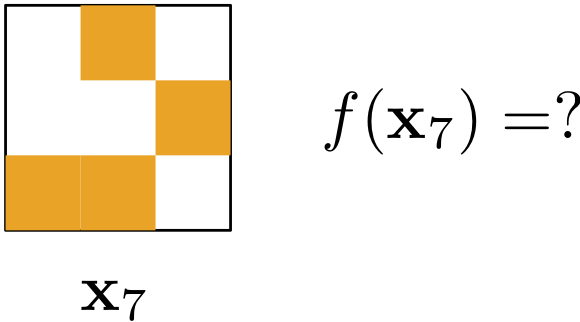
- Learning seems impossible without additional assumptions!
Possible vs probable

Flip a biased coin, lands on head with unknown probability \(p\in[0,1]\)
\(\P{\text{head}}=p\) and \(\P{\text{tail}}=1-p\)
Say we flip the coin \(N\) times, can we estimate \(p\)?
\[ \hat{p} = \frac{\text{# head}}{N} \]
Can we relate \(\hat{p}\) to \(p\)?
- The law of large numbers tells us that \(\hat{p}\) converges in probability to \(p\) as \(N\) gets large \[ \forall\epsilon>0\quad\P{\abs{\hat{p}-p}>\epsilon}\mathop{\longrightarrow}_{N\to\infty} 0. \]
It is possible that \(\hat{p}\) is completely off but it is not probable
Components of supervised machine learning
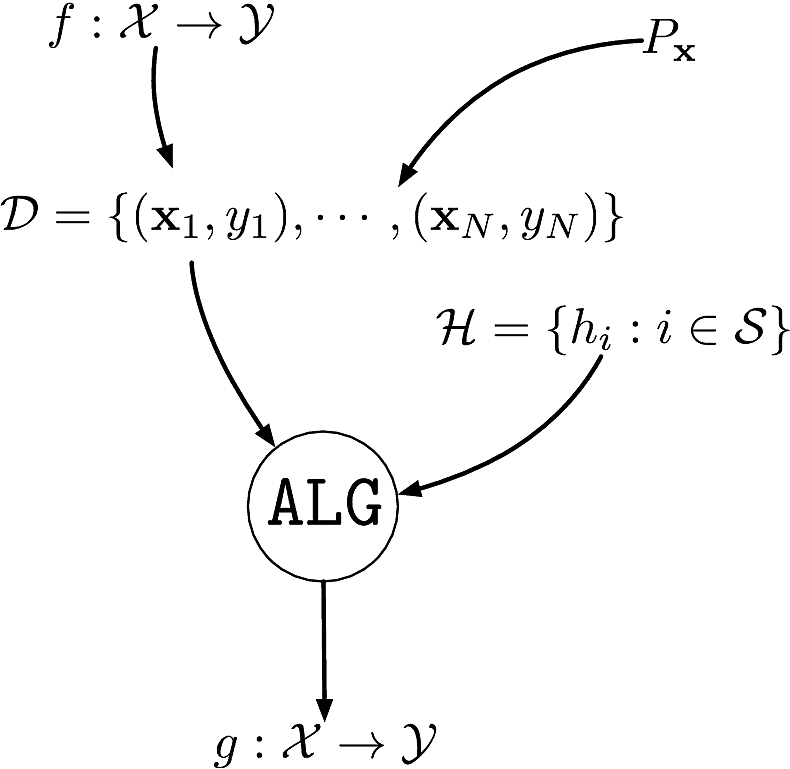
An unknown function \(f:\calX\to\calY:\bfx\mapsto y=f(\bfx)\) to learn
A dataset \(\calD\eqdef\{(\bfx_1,y_1),\cdots,(\bfx_N,y_N)\}\)
- \(\{\bfx_i\}_{i=1}^N\) i.i.d. from unknown distribution \(P_{\bfx}\) on \(\calX\)
- \(\{y_i\}_{i=1}^N\) are the corresponding labels \(y_i\in\calY\eqdef\bbR\)
A set of hypotheses \(\calH\) as to what the function could be
An algorithm \(\texttt{ALG}\) to find the best \(h\in\calH\) that explains \(f\)
Another learning puzzle

Components of supervised machine learning
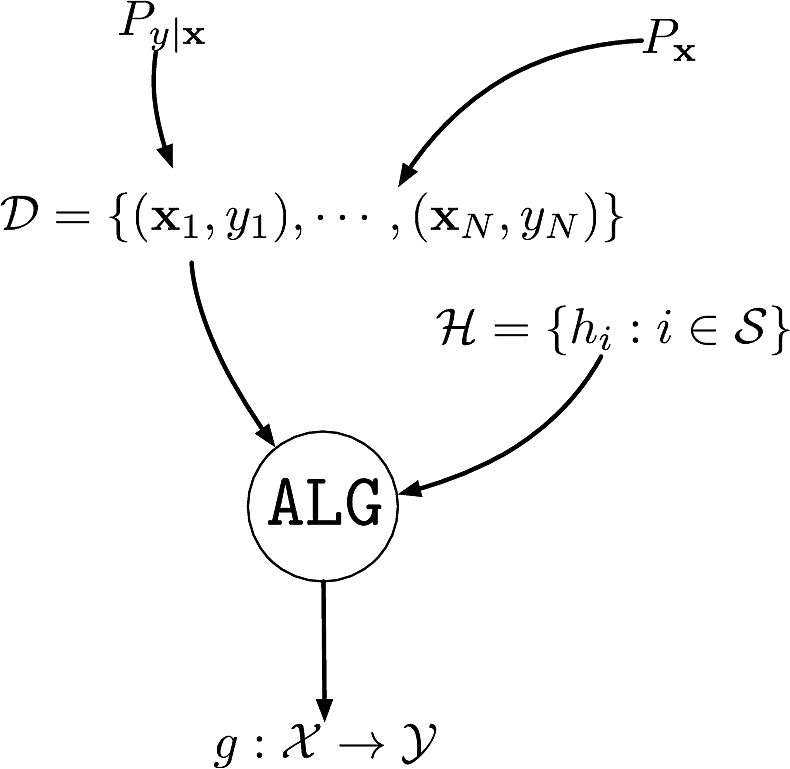
::: nonincremental
An unknown conditional distribution \(P_{y|\bfx}\) to learn
- \(P_{y|\bfx}\) models \(f:\calX\to\calY\) with noise
A dataset \(\calD\eqdef\{(\bfx_1,y_1),\cdots,(\bfx_N,y_N)\}\)
- \(\{\bfx_i\}_{i=1}^N\) i.i.d. from distribution \(P_{\bfx}\) on \(\calX\)
- \(\{y_i\}_{i=1}^N\) are the corresponding labels \(y_i\sim P_{y|\bfx=\bfx_i}\)
A set of hypotheses \(\calH\) as to what the function could be
An algorithm \(\texttt{ALG}\) to find the best \(h\in\calH\) that explains \(f\) :::
- The roles of \(P_{y|\bfx}\) and \(P_{\bfx}\) are different
- \(P_{y|\bfx}\) is what we want to learn, captures the underlying function and the noise added to it
- \(P_{\bfx}\) models sampling of dataset, need not be learned
Yet another learning puzzle

- Assume that you are designing a fingerprint authentication system
- You trained your system with a fancy machine learning system
- The probability of wrongly authenticating is 1%
- The probability of correctly authenticating is 60%
- Is this a good system?
- It depends!
- If you are GTRI, this might be ok (security matters more)
- If you are Apple, this is not acceptable (convenience matters more)
- There is an application dependent cost that can affect the design
Components of supervised machine learning
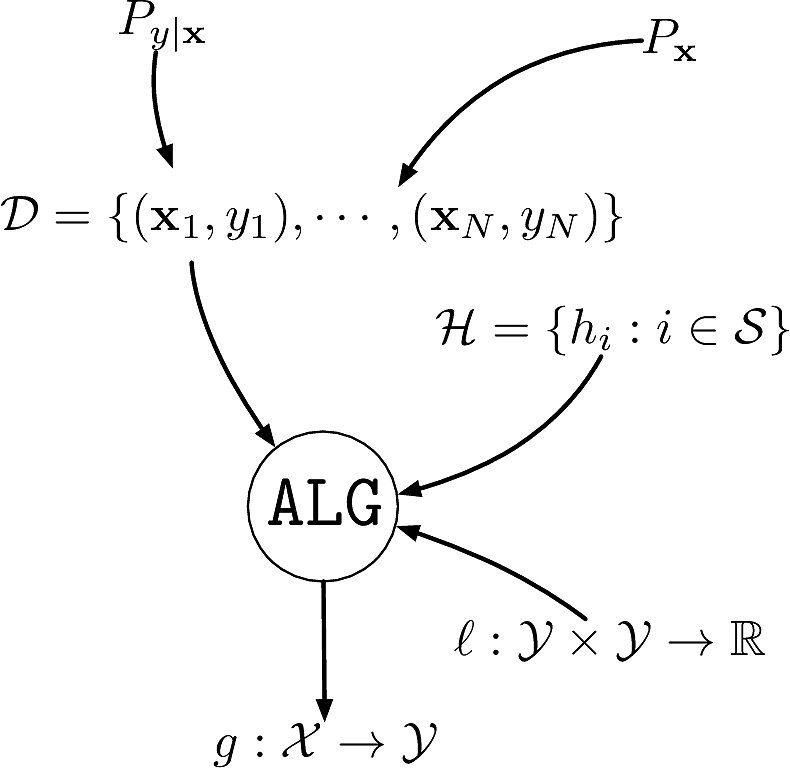
A dataset \(\calD\eqdef\{(\bfx_1,y_1),\cdots,(\bfx_N,y_N)\}\)
- \(\{\bfx_i\}_{i=1}^N\) i.i.d. from an unknown distribution \(P_{\bfx}\) on \(\calX\)
An unknown conditional distribution \(P_{y|\bfx}\)
- \(P_{y|\bfx}\) models \(f:\calX\to\calY\) with noise
- \(\{y_i\}_{i=1}^N\) are the corresponding labels \(y_i\sim P_{y|\bfx=\bfx_i}\)
A set of hypotheses \(\calH\) as to what the function could be
A loss function \(\ell:\calY\times\calY\rightarrow\bbR^+\) capturing the “cost” of prediction
An algorithm \(\texttt{ALG}\) to find the best \(h\in\calH\) that explains \(f\)