Mathematical Foundations of Machine Learning

Last time

• Last class: Monday November 25, 2024
  • We talked about Maximum likelihood estimation
• Today: We will talk about principal component analysis
  • Great way to end the course where we started
• To be effectively prepared for today's class, you should have:
  1. Gone over slides and read associated lecture notes here and there and there
  2. Submitted Homework 8

Final exam is coming

• Review all notes and exams: exam is comprehensive
  • Friday December 6, 2024 2:40pm-5:30pm (see https://registrar.gatech.edu/info/final-exam-matrix-fall-2024)
  • In class and open notes
  • Same rules as for the midterm with electronics
• Frequently asked questions
  • How many problems on the midterm?
  • How many questions on the midterm?
  • What topics will the midterm cover?
  • Do you have sample exams?
  • Can we do additional work for extra credit?
  • Do you give bonuses for participation or for CIOS completion?
• We will be very available for help and review sessions
  • Tuesday December 03, 2024 12pm: Anuvab (hybrid)
  • Wednesday December 04, 2024 9am: Dr. Bloch (online)
  • Wednesday December 04, 2024 11:30am: Jack (online)

Back to first lecture: Kernel PCA

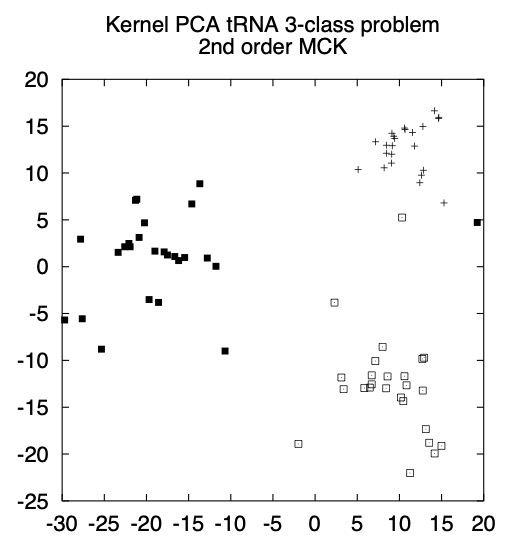
• tRNA (transfer RNA): plays a key role in the creation of amino acid sequence of proteins (source)
  • G G G G A A T T A G C T C A A G C G G T A G A G C G …
• Challenge: compare, classify, analyze, visualize sequences
  • Datasets of tRNA sequences ${\{{\mathbf{x}}_i\}}_{i=1}^n$
• Lots happening behind the scene
  • What does it mean to represent the data in 2D?
  • How do we measure distances between tRNA sequences?
  • We can explain a lot now!

Principal Component Analysis

• Feature extraction methods based: unsupervised, linear, based on sum of square errors

• Idea is to find approximation of data as $${\mathbf{x}}_i\approx \mathit{\mu }+\mathbf{A}{\mathit{\theta }}_i\mathsf{\text{ with }}\mathit{\mu }\in {\mathbb{R}}^d,\mathbf{A}\in {\mathbb{R}}^{d\times k},{\mathit{\theta }}_i\in {\mathbb{R}}^k$$ and $\mathbf{A}$ has orthonormal columns

• Hard part is finding $\mathbf{A}$

• Given $\mathbf{A}$, relatively easy to find ${\mathit{\theta }}_i$ and $\mathit{\mu }$

Solving PCA

Solving PCA

• Proof steps
  • Step 1: introduce $\mathbf{S}\triangleq \sum _{i=1}^N{\mathbf{x}}_i{\mathbf{x}}_i^{⊺}=\mathbf{X}{\mathbf{X}}^{⊺}$
  • Step 2: introduce linear program
  • Step 3: solve linear program
• Connection to SVD $\mathbf{X}=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^{†}$ where columns of $\mathbf{X}$ are ${\mathbf{x}}_i-\mathit{\mu }$: $$\mathbf{X}=\underset{\mathbf{U}}{\underbrace{\left[\begin{array}{ccc}|& & \\ \mathbf{A}& & \\ |& & \end{array}\right]}}\underset{\mathrm{\Sigma }{\mathbf{V}}^{†}}{\underbrace{\left[\begin{array}{c}-\mathrm{\Theta }-\\ \end{array}\right]}}$$

Kernel PCA